電気を通しやすい導体と
電気を通さない絶縁体（不導体）。

この違いはなんなのか。

まずは、
導体の代表格、金属の仕組みを見てみましょう。

金属の結合

水と電気の関係。純水は電気を通さない？（電気の基礎知識）では共有結合について。
イオンとは？日常でよく耳にするイオンの正体（電気の基礎知識）ではイオン結合についてご説明しましたが、

物質の結合の仕方にはもう一つ種類があります。

それが、
イオン結合によく似ている結合で＜金属結合＞といいます。

その名の通り
金属元素が結合する方法のことを言うのですが、
金属が持つ光沢や熱伝導性といった特徴は、
この金属結合によってもたらされるのです。

この金属結合を
銅の原子でご説明していきたいと思います。

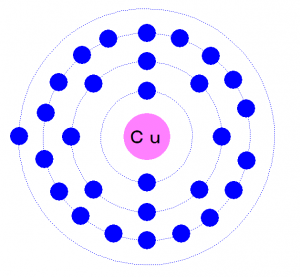
銅原子は、
最外殻に一つだけ電子が余っている状態なので、
この電子を放出して安定した状態になろうとします。

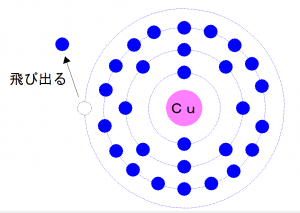
（－）の電荷を持つ電子を放出するので、
銅の原子は電気的に中性の状態から（＋）になりプラスイオンになります。

このままではイオン化して終わりなのですが、
この銅の原子がたくさんある状態ではどうなるでしょうか？

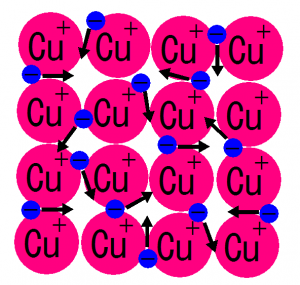
銅のプラスイオンの周りを電子が移動し、
自由に泳ぎ回っているような状態になります。

この泳ぎ回る電子はもちろん（－）の電荷を持っているので、
（＋）の電荷を持つ銅イオンは
クーロン力によって電子に引き付けられ結合します。

それでも電子は動き続けるので
この動き回る電子ととっかえひっかえ波打つように
銅イオンは結合します。

このように、
動き続ける電子とクーロン力によって結合することを
金属結合といいます。

自由電子が絶えず動き回るので
金属は電気を非常に通しやすい導体となるのです。

また、
動き回る電子によって結合されているので
外部から力を加えられ曲がったり伸ばされたりしても
原子レベルでの結合にはなんら支障はありません。

これが金属特有の展性や延性の良さの正体です。

金属の導電率（消防設備士試験　出題率・中）

電気の通りやすさを導電率といいますが、
金属を導電率の高い順番で並べると、

銀＞銅＞金＞アルミニウム＞鉄＞白金

となります。

銀は非常に高価な為、
電線などには安価な銅が用いられています。

アルミニウムは、
銅よりも導電率で劣りますが、その軽さから送電線の素材として使われています。

こちらは消防設備士試験で出やすい部分ですので、
ぜひ覚えていただければと思います。

絶縁体とは

電気を通さない絶縁体は、
電子の束縛が強い＜共有結合＞によって結合された物質です。

純水は水素と酸素の共有結合なので電気を通しません。

その他、

ガラス。

漫画「ワンピース」の主人公・ルフィでお馴染みの、ゴム。
（空島編で雷人間エネルと闘いましたね。）

などがあります。

絶縁体は電気を全く通さないわけではなく、
非常に高い電圧を与えてやると
電子の束縛が破られ絶縁破壊を起こし、電気が流れるようになります。

雷がその代表例です。

導体の抵抗率（消防設備士試験　出題率・高）

導体の抵抗は、
それぞれの導体が持つ特有の抵抗率と長さに比例して大きくなり、
断面積に反比例して小さくなります。

電気が流れる。

つまり、
導体の中を電子が移動する際、
電子は導体を構成する元素の原子核にぶつかりながら移動します。

このぶつかりによって電子の移動の妨げになることを
導体が持っている抵抗（抵抗率）といいますが、

この抵抗率は、
パチンコをイメージしていただければと思います。

パチンコ玉を電子とすると、

釘が多ければ、
玉が釘にぶつかって跳ね返り、落ちてくるまでに時間がかかります。

釘が少なければ、
跳ね返りが少なく、すぐに玉は落ちてきます。

導体の長さは、
ホースのようなものをイメージしてもらえればと。

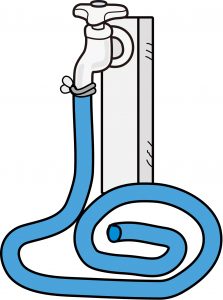
ホースが短ければ、
水はすぐさま出てきますし、勢いもそのままです。

しかしホースが長ければ長いほど、
水が出てくるのに時間がかかるのと、
ホースとの摩擦によって勢いは弱まります。

導体の断面積は、
砂時計をイメージしてください。

砂の通る穴が細ければ、
砂の落ちる量が少なくなり全て落ちるまでに非常に時間がかかります。

一方、
穴が太ければ砂はあっという間に落ちてきます。

導体の抵抗をＲ、抵抗率をρ、長さをＬ、断面積をｓとすると

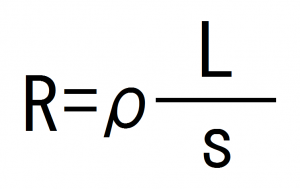
このように表すことができます。
これは重要ですのでぜひ覚えてください。

また、
時折、断面積を直径に変えて出題してくることもあります。
その場合は、
断面積＝半径×半径×πなので、直径Ｄで表すと、

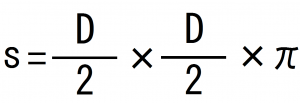
となり、
これを計算すると、

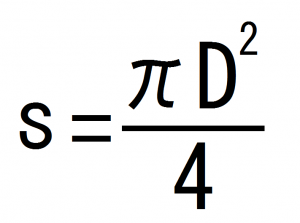
最初の式に、
これを代入すると

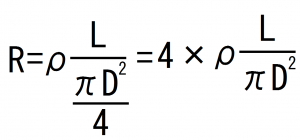
この式から、
導体の抵抗Ｒは、
長さＬに比例して、直径の２乗に反比例する。

というのがわかります。

試験の際に慌てないよう、
これも頭に入れてもらえればと思います。

以上、
導体と絶縁体についてでした。